Search-Problem的形式化描述
对于一个planning-agent,设立一个目标goal以满足其最大化性能,如果Agent达到了goal,我们的Search-Problem也就得到了解决;
第一步就是要形式化地描述这个Agent的性能度量,一般地,对于一个Search-Problem来说,有几个要素:
- a state space:状态空间
- a successor function:转移模型
{action, costs}描述状态a通过某个行动转移到状态b以及可能的代价的函数; - a initial state:初始状态
- a goal test
如果我们称一个Search-Problem找到了solution,也就是找到了一个行动序列,或者说一个plan,从初始状态移动到目标状态,这样的找到solution的过程称为搜索;
所有的Search-Problm都是模型Model;
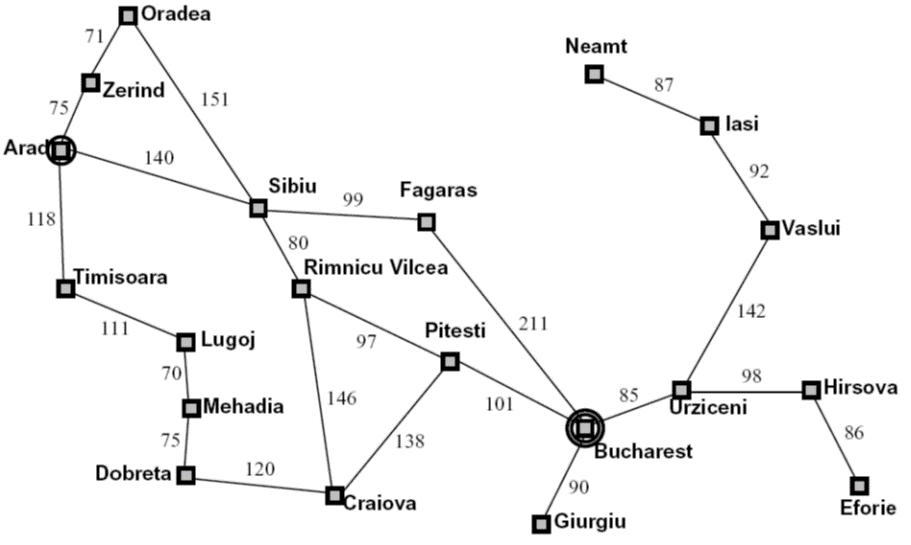
Romania Map Example
对于Agent在Romania的Arad旅游,可以如下地形式化描述:
-
State space:Cities
-
Successor function:
- Roads: Go to adjacent city
- cost:distance
-
Start state:Arad
-
Goal test: Is state == Bucharest?
-
Solution?
Search Space Graphs&Search Trees
一个搜索算法需要考虑各种可能的行动序列,而状态图就是搜索问题的数学描述,每个状态在状态图仅出现一次形成结点,而搜索过程往往是沿着图中的一棵树上进行的;
- 根节点从初始状态出发;
- 结点表示状态空间的状态;
- 连线表示行动,一次合法的行动将会拓展当前状态,生成一个新的状态集,也就是从父节点出发得到如若干子节点;
- 给定某个搜索时刻。还没展开的叶节点称为边缘;
- 选择展开的结点的顺序就是搜索策略;
我们往往很难在内存中将状态图存储,甚至对大多数问题,我们也没必要真的建立整棵搜索树;
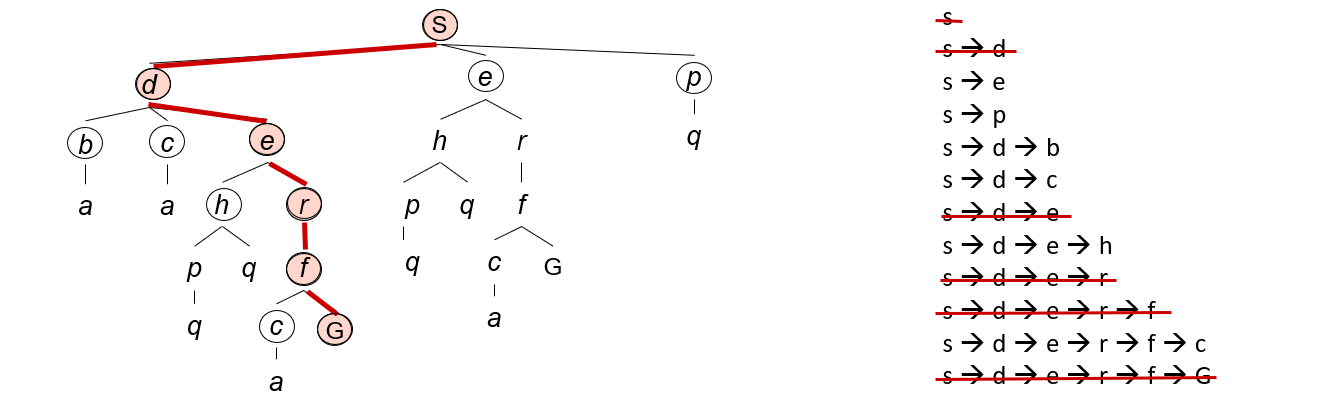
下面是一个例子来描述状态图和搜索树的;
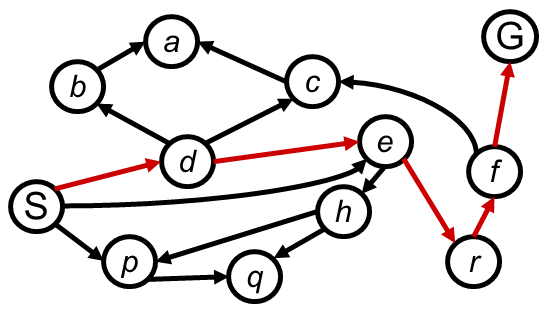

在搜索过程中,有些冗余状态和冗余路径是不可避免的,但是可能状态是有限的,因此那些遗忘搜索历史的算法可能会不幸地重复历史;
引入探索集(closed表,fringe),记录每个已拓展地结点,常用Hash表实现,加入Hash表的数据结构一定要是可哈希的,比如对于numpy.ndarray,可以用tobites()方法转化成字节序列,这是一个可哈希的数据结构;
在搜索算法中我们要选择下一个拓展的结点,比较合适的数据结构是队列,包括FIFO队列(Queue),LIFO队列(Stack),优先队列(priority_queue);
General Tree Search
对于通用搜索树来说,有三点需要注意:
- Fringe
- Expansion
- Exploration strategy
关注解决哪个结点是需要拓展的问题,算法的性能有一个考量:
- 完备性:是否能找到解?
- 最优性:是否能找到最优解(最小代价)?
- 时间复杂度;
- 空间复杂度;
对于上述例子的搜索过程,我们可以这样表示它的过程;