Preface
这是7.10的比赛,爆零告终;
今天训练赛的GH题来自下面这场比赛的A题和C题:
https://codeforces.com/gym/103466
其余题来源于:
https://codeforces.com/gym/104197
第二个链接可以在下图位置找到其余题的题解;
Content
A. Adjacent Product Sum
题意:
给定n个正整数,希望重新排列而最大化相邻两项乘积循环和sum(a)=\sum_{i=1}^{n}a[i]a[i+1]
思路:
这样的循环和让人一眼想起女奥不等式,但是这里变量的取值都是固定的,所以不难想起使用局部调整法;
考察序列最大值M,和次大值A,B,若A,B不位于M的两侧,那么调整为M的两侧sum(a)不减(排序不等式),设M两侧的数为a,b,A,B两侧的数为c,d,e,f:
那么sum(a)=sum(a-{M})+M(A+B)-AB,变元个数递降,取等条件如图所示,用i来表示序列中第i小的数;
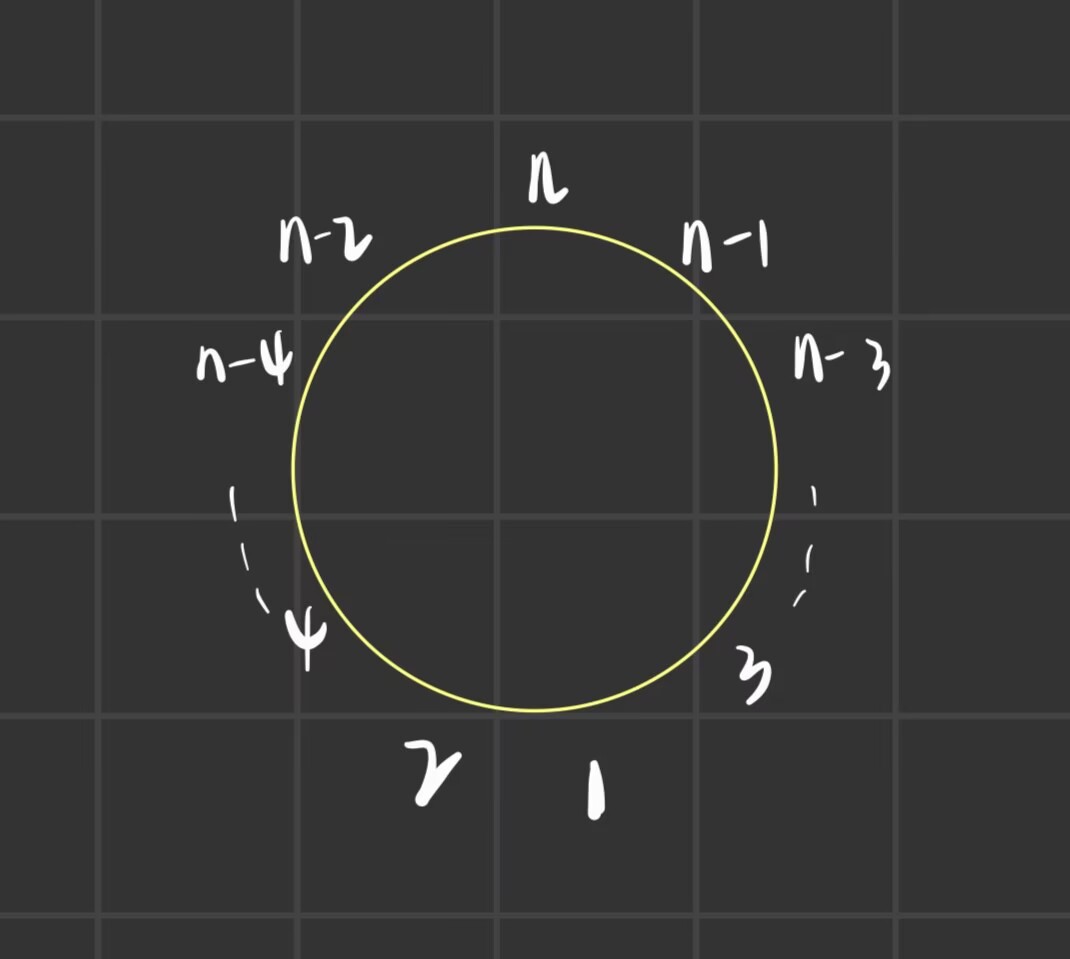
在调试的时候一直超时,当时也弄不明白什么原因,后来把数组开成int就过了,由于这道题的输入量很大,微小的效率问题都可能会超时,能开int一定不要开long long,不能开的一定要大胆开long long
AC code:
#define local
#include<bits/stdc++.h>
using namespace std;
const int maxn=200005;
typedef long long ll;
int main(){
#ifdef local
freopen("in.txt","r",stdin);
freopen("out,txt","w",stdout);
#endif
int t;
scanf("%d",&t);
while(t--){
int n;
scanf("%d",&n);
int a[maxn];
memset(a,0,sizeof(a));
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
}
ll ans=0;
sort(a,a+n);
int order[n+1]={0};
for(int i=1;i<n;i++){
if(i&1)
order[(i>>1)+1]=i;
else
order[n-(i>>1)]=i;
}
order[n]=0;
for(int i=0;i<n;i++){
ans+=1LL*a[(order[i])]*a[order[(i+1)%n]];
}
printf("%lld\n",ans);
}
return 0;
}
B. Distance Parities
题意:
给定连通图两两顶点最小距离的奇偶性,判断是否存在这样满足条件的图;
思路:
由于根本没有见过这种可能多解的问题卡了很久,事实上我们只需要给出自己的构造就好了;
我们注意到临界矩阵天然满足这样的奇偶性关系,我们假定输入的就是邻接矩阵,利用Floyd算法检查奇偶性是否成立,如果可以就还原原图,如果不行答案就是否定的;
AC code:
#define local
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
const int maxn=505;
int a[maxn][maxn];
long long dis[maxn][maxn];
const long long INF= (1<<30)-1;
void Floyd(int n,long long (&dis)[maxn][maxn]){
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
dis[i][j]=std::min(dis[i][j],dis[i][k]+dis[k][j]);
}
}
}
return ;
}
int main ()
{
#ifdef local
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
int t;
cin>>t;
while(t--){
int n;
cin>>n;
memset(a,0,sizeof(a));
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
scanf("%1d",&a[i][j]);
}
}
long long dis[maxn][maxn];
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(a[i][j]) dis[i][j]=1;
else dis[i][j]=INF;
}
}
Floyd(n,dis);
int ans=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(a[i][j]==1&&dis[i][j]%2==0) ans=0;
if(a[i][j]==0&&dis[i][j]%2==1) ans=0;
}
}
if(ans==0) cout<<"NO"<<endl;
else {
cout<<"YES"<<endl;
int cnt=0;
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
if(a[i][j]==1) cnt++;
}
}
cout<<cnt<<endl;
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
if(a[i][j]==1) cout<<i<<" "<<j<<endl;
}
}
}
}
return 0;
}
C. Excellent XOR Problem
题意:
询问是否能将给定数组划分为若干(至少两个)异或和不同的子数组,若答案是肯定的则给出构造;
思路:
由于题目的条件非常的弱,我们猜想可能不需要划分成很多子数组因为数量越多可能就约有可能出现相同的异或和,称题目划分异或和不同的子数组的操作为「合法的」;
尝试划分为两个,假如不能划分为两个,说明在任意位置分割原数组,左右两边的异或和都相等;
注意异或和的性质:A\wedge A=0,A\wedge 0=A; 换言之,若A\wedge B=C
- 若A不等于B,那么C也不可能是0
- 若C不等于0,A,B也不可能相等;
注意后面的性质实际上就是一种分拆方案,考虑数组全体的异或和sum,划分为两个如果是「非法的」,等价于sum=0;相反如果划分两个子数组是「合法的」,我们只需要取出第一个数和剩下的数就好了;
假如sum=0,我们退而求其次希望能够划分为三个子数组P,Q,R,我们找到原数组的前缀异或和,如果幸运地找到(第)一个非零的数x(如果找不到说明原数组和前缀异或和全都是零,答案就是否定的),假设在第i个位置非零,在位置小于i前缀异或和必定都是零,我们把前i个数加入P,P的异或和为x;
此时Q,R的全体的异或和也是x不为0,考虑到Q的异或和表现为从i+1开始的前缀异或和,从i+1开始更新持续加入当前位置的数,找到一个既不为0也不为x的,第i+1位置往后的前缀异或和就完成了(如果找不到,说明整个数组不是0就是x,那划分更多的数组也做不到「合法」,答案是否定的);
当时被A卡爆了,题目是后面补的;
AC code:
#define local
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
const int INF=1<<30;
const int maxn=200005;
void solution(){
int n;
cin>>n;
vector<int> a(n+1);
int fa=0;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) fa^=a[i];
if(fa==0) {
int i=0;
for(i=1;i<=n;i++) if(a[i]!=0) break;
if(i==n+1) {
cout<<"NO"<<endl;
return;
}
else {
int j=i+1;
int x=a[i];
int y=0;
for(j=i+1;j<=n;j++){
y^=a[j];
if(y!=0&&y!=x) {
cout<<"YES"<<endl;
cout<<3<<endl;
cout<<1<<" "<<i<<endl;
cout<<i+1<<" "<<j<<endl;
cout<<j+1<<" "<<n<<endl;
return;
}
}
if(j==n+1) {
cout<<"NO"<<endl;
return ;
}
}
}
else {
cout<<"YES"<<endl;
cout<<2<<endl;
cout<<1<<" "<<1<<endl;
cout<<2<<" "<<n<<endl;
return ;
}
return ;
};
int main ()
{
#ifdef local
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
int t;
cin>>t;
while(t--) solution();
return 0;
}
D. Increasing Grid
题意:
给定一个初始已经填了若干个数的n\times m表格,求解能让这个表格从左上到右下严格递增,所有数不小于1,不超过n+m的填表方案数;
思路:
一眼每个数s[i][j]其实只有两种取值i+j-1,i+j,如果是前者那么他左上角的数一定全部都是取较小的数,如果是后者它右下角的数一定全部都是取较大的数,所以暂且不论没填的数,如果填的数不是这两个中的一个那肯定方案数就是0了(否则最左上角或者最右下角的数就要超出[1,n+m]的范围了),所以我么们让a[i][j]减去i+j-1,整张表就是-1,0,1表了;
按照这个思路我们先尽可能地填表,如果填表产生了矛盾说明不存在这样的方案;
现在还剩下一些没有填表的数,问题转化为找到这样一条从左下到右下的0-1分界线,这是非降路径计数问题,类似于Catalan数的求解,对还填着-1的格子dp即可;
一定要记得取模!
AC code:
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
const int mod=998244353;
void solution(){
int n,m;
cin>>n>>m;
vector<vector<int>> a(n+1,vector<int>(m+1));
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(a[i][j]==-1) continue;
a[i][j]-=(i+j-1);
if(a[i][j]!=0&&a[i][j]!=1) {
cout<<0<<endl;
return ;
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(a[i][j]!=1) continue;
if(i+1<=n){
if(a[i+1][j]==0) {
cout<<0<<endl;
return ;
}
a[i+1][j]=1;
}
if(j+1<=m) {
if(a[i][j+1]==0){
cout<<0<<endl;
return ;
}
a[i][j+1]=1;
}
}
}
for(int i=n;i>=1;i--){
for(int j=m;j>=1;j--){
if(a[i][j]!=0) continue;
if(i-1>=1) {
if(a[i-1][j]==1){
cout<<0<<endl;
return ;
}
a[i-1][j]=0;
}
if(j-1>=1){
if(a[i][j-1]==1)
{
cout<<0<<endl;
return ;
}
}
a[i][j-1]=0;
}
}
vector<vector<ll>> dp(n+1,vector<ll> (m+1));
dp[n][0]=1;
for(int i=n;i>=0;i--){
for(int j=0;j<=m;j++){
if(i+1<=n){
if(j==0&&a[i+1][j+1]!=0) dp[i][j]+=dp[i+1][j];
else if(j==m&&a[i+1][j]!=1) dp[i][j]+=dp[i+1][j];
else if(j>0&&j<m&&a[i+1][j+1]!=0&&a[i+1][j]!=1) dp[i][j]+=dp[i+1][j];
dp[i][j]%=mod;
}
if(j>0){
if(i==n&&a[i][j]!=1) dp[i][j]+=dp[i][j-1];
else if(i==0&&a[i+1][j]!=0) dp[i][j]+=dp[i][j-1];
else if(i>0&&i<n&&a[i][j]!=1&&a[i+1][j]!=0)dp[i][j]+=dp[i][j-1];
dp[i][j]%=mod;
}
}
}
cout<<dp[0][m]%mod<<endl;
}
int main ()
{
#ifdef local
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
int t;
cin>>t;
while(t--) solution();
return 0;
}
E. Jewel of Data Structure Problems
题意:
给定[n]的置换和多组询问,回答每次交换操作后的序列最长奇子序列的长度;
思路:
- 注意到如果序列是奇排列,那么那么最长的就是自己;
- 如果序列是自然排列,那么是没有奇子序列的;
- 如果序列是偶排列,如果我们能删去一个对逆序数贡献为奇数的数,那么删去这个数就可以得到奇排列;
- 如果找不到这样的数,那么就要考虑删去更多的数,观察样例,猜想是否能删去两个数得到奇排列;
- 我们有定理:对于长度为n的偶置换\phi:\phi_1,\phi_2,...,\phi_n,假设在\phi中下标小于k的,比\phi_k大的数有a_k个,比\phi_k小的数有k-1-a_k个;下标大于k的,比\phi_k小的数有b_k个,比\phi_k大的数有n-k-b_k个;
-
- 如果存在k,使得\phi_k-k为奇数,那么最长奇子序列长度为n-1;如果不存在,说明\phi_k-k全为偶数,删去两个数,由容斥原理,这两个数相关的逆序对要么都没计算要么计算两遍,要计算回来的话总逆序对数变化为奇数,那么序列最长奇子序列的长度为n-2;
AC code:
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
const int maxn=2e5+5;
class Segment_tree{
public:
int n;
vector<int> tr;
Segment_tree(int _n){ int w=1;
n=_n;
while(w<n) w<<=1;
w<<=1;tr.resize(w+1,0);
}
void update(int v,int l,int r,int i,int x){
if(l==r){
tr[v]=x;
return ;
}
int m=l+((r-l)>>1);
if(i<=m) update(2*v,l,m,i,x);
else update(2*v+1,m+1,r,i,x);
tr[v]=tr[2*v]+tr[2*v+1];
}
int get(int v,int x,int y,int l,int r){
if(y<l||x>r)return 0;
if(l<=x&&y<=r) return tr[v];
int m=x+((y-x)>>1);
return get(2*v,x,m,l,r)+get(2*v+1,m+1,y,l,r);
}
};
int calc(int n,vector<int>&a){
Segment_tree t=Segment_tree(n+1);
int cnt=0;
for(int i=1;i<=n;i++){
if(a[i]<n) cnt+=t.get(1,1,n,a[i]+1,n);
t.update(1,1,n,a[i],1);
}
return cnt;
}
int main ()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#ifdef local
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
int n,q;
cin>>n>>q;
int good=0 ,cnt=0;
vector<int> p(n+1);
for(int i=1;i<=n;i++) {
cin>>p[i];
if(p[i]==i) good++;
if((p[i]-i)%2) cnt++;
}
int sta=calc(n,p)%2;
while(q--){
sta^=1;
int u,v;
cin>>v>>u;
if(p[v]==v) good--;
if(p[u]==u) good--;
if((p[v]-v)%2) cnt--;
if((p[u]-u)%2) cnt--;
swap(p[v],p[u]);
if(p[v]==v) good++;
if(p[u]==u) good++;
if((p[v]-v)%2) cnt++;
if((p[u]-u)%2) cnt++;
if(good==n) cout<<-1<<endl;
else {
if(sta) cout<<n<<endl;
else {
if(cnt) cout<<n-1<<endl;
else cout<<n-2<<endl;
}
}
}
return 0;
}
F. King of Swapping
题意:
给定长度为n的置换p,给定一系列由两个数a,b决定的操作:如果p_a>p_b,则可以交换p_a,p_b,判断这些操作的组合能否做到置换间的相互转化;
思路:
首先只要任意序列能做到与自然排列的相互转化,那么答案就是肯定的,否则是否定的;
我们考虑对操作的两个数连有向边,只需说明这个图是强连通的,也即这个图的强连通分量个数为1;




