Hash技术

Background

大数据挖掘面临的问题：

高维诅咒：比如K-dTree无法处理高维问题；
存储问题
检索速度问题

Hash技术致力于解决这个问题，也是Hash技术的作用；

Content

K-Shingles技术

-Shingle：连续个字符一起出现的序列；

通过-shingle技术，可以很方便地将文档存储成一个列表，进行后续操作；

签名矩阵与最小哈希(MinHashing)

现有一个矩阵，有列（记录个文档），列的长度也很长；

我们希望对列C作Hash，转化为签名,有如下性质：

对于两列,相似性，解决检索速度问题；
对降维，解决存储问题和维度诅咒问题；

将表示为长度为的布尔向量，有的元素标记为1，没有标记0，那么计算两个集合(列)的Jaccard相似度：

其中两个集合的同一个元素的存在情况有如下四种，分别计数:

定义最小哈希函数：集合中第一个出现1的索引；

下图是一个例子，permulation是三个对索引的全排列；

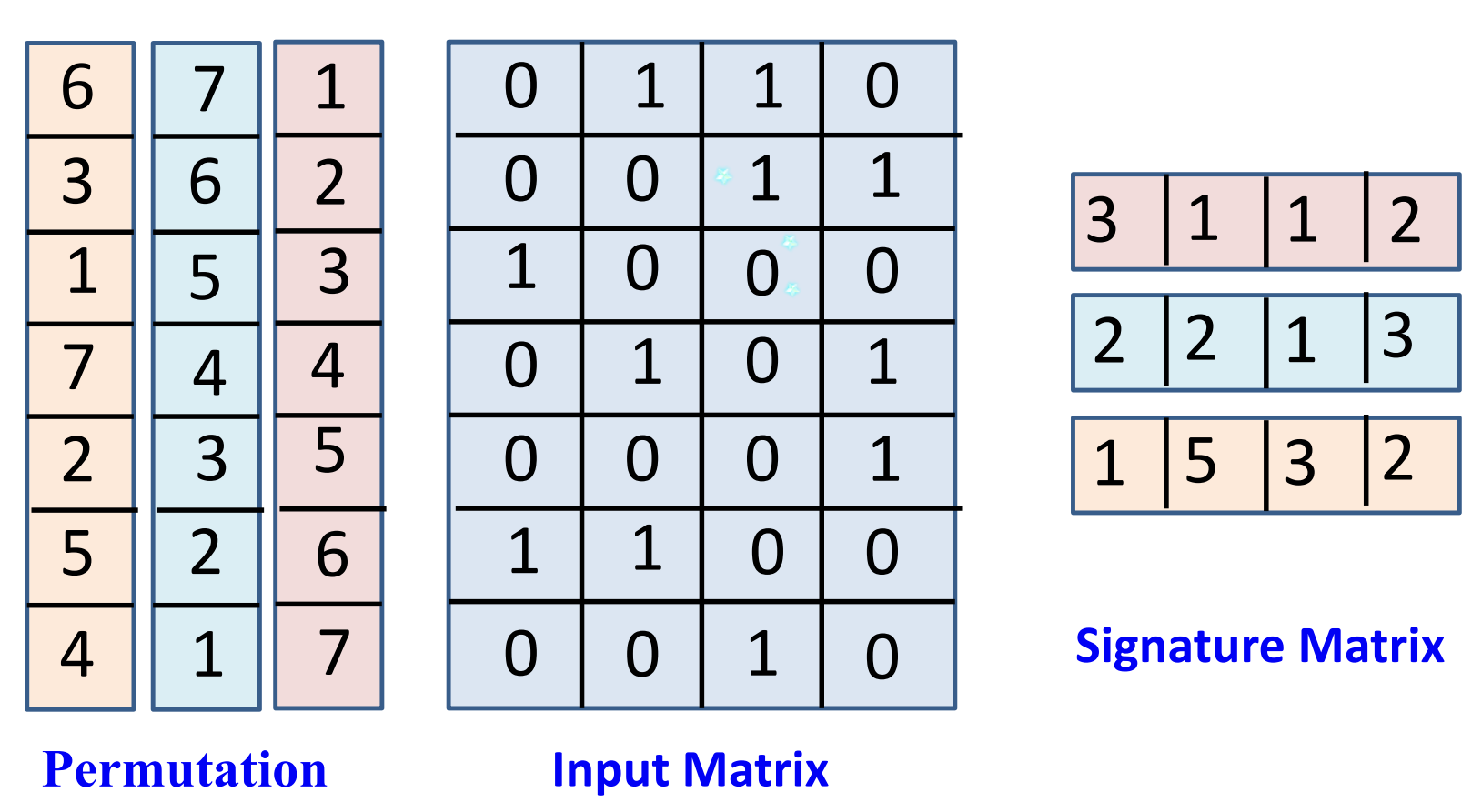
可以看到，生成签名矩阵并不会对输入矩阵打乱；

对于两列，事件表示在随机的索引全排列为下，最小哈希值相等;

从索引1开始看到索引，检查列，直到我们第一次发现了1，它只能是type a的情况之于type a,type b,type c，因此也就是相似性；

我们准备很多个的全排列，对于固定的输入矩阵，最小哈希函数对不同的索引排列将产生不同的行结果,将签名矩阵看成结果的vector;

我们如何准备这些全排列呢？答案还是哈希。

对于的全排列，哈希函数会将这个排列映射成的排列;

注意，我们并不是得出整个索引排列之后，再找那个出现1最早的索引，而是不断的更新签名矩阵：

初始化签名矩阵为无穷大；
遍历所有行;对固定的行，遍历所有的列；
对于固定的列,如果第行有1；
对每个准备好的Hash函数，计算;
更新

一个文档的签名指的是[M(0,c),M(1,c),...]

局部敏感哈希(Locality-Sensitive Hashing)

我们也许要准备很多个全排列，也就是很多个hash函数，这样才能用大数定律，以频率估计概率，从而估计相似性；

也就是说，我们的签名矩阵终于能降维到被内存装下了，但是找到相似文档依然不可能线性查找枚举所有可能的文档对，代价是；

LSH 将原始数据空间中的两个相邻数据点通过相同的映射或投影变换（projection）后，这两个数据点在新的数据空间中仍然相邻的概率很大，而不相邻的数据点被映射到同一个桶的概率很小。也就是说，如果我们对原始数据进行一些hash映射后，我们希望原先相邻的两个数据能够被hash到相同的桶内，具有相同的桶号。这样只需要计算两个数据点的hash值是否在同一个桶里就能判断它们是否大概率相似；

这和普通的hash的设计带来的蝴蝶效应不同（混沌系统微小初值改变引起巨大变化），它不希望hash冲突；

但是对LSH来说，目的就是要创造更多的冲突，但本来相似的对象hash完很不相似，或者不相似的的对象hash完映射到一个桶的情况仍不可避免；

关键要找到这么一个性质的LSH函数，略.

一个trick：