1547 - Scarborough's Fair

题目

[Leetcode 1547](1547. 切棍子的最小成本 - 力扣（LeetCode）)

切棍子的最小成本

有一根长度为 n 个单位的木棍，棍上从 0 到 n 标记了若干位置。例如，长度为 6 的棍子可以标记如下：

给你一个整数数组 cuts ，其中 cuts[i] 表示你需要将棍子切开的位置。

你可以按顺序完成切割，也可以根据需要更改切割的顺序。

每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根木棍的长度和就是切割前木棍的长度）。请参阅第一个示例以获得更直观的解释。

返回切棍子的 最小总成本 。

示例 1：

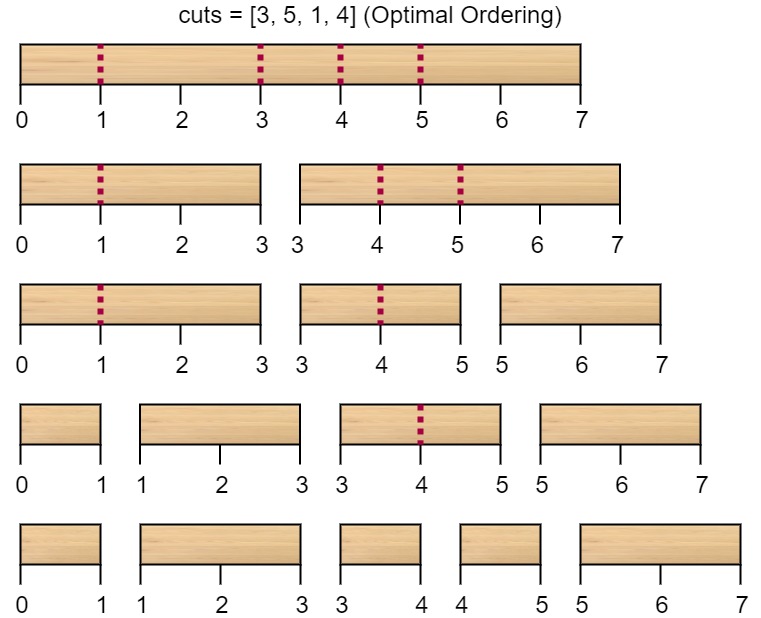
输入：n = 7, cuts = [1,3,4,5]
输出：16
解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示：

第一次切割长度为 7 的棍子，成本为 7 。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。
而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。

示例 2：

输入：n = 9, cuts = [5,6,1,4,2]
输出：22
解释：如果按给定的顺序切割，则总成本为 25 。总成本 <= 25 的切割顺序很多，例如，[4, 6, 5, 2, 1] 的总成本 = 22，是所有可能方案中成本最小的。

提示：

2 <= n <= 10^6
1 <= cuts.length <= min(n - 1, 100)
1 <= cuts[i] <= n - 1
cuts 数组中的所有整数都 互不相同

题解

明显能想到，尽管随着cuts顺序变化，但是最终剩余的原子棍子都是固定的，因此应该考察一个逆向问题，合并这些短棍子具有某种代价，现找到一种方案使得代价最小化；

第len个阶段，我们合并len个棍子，可以看到，每个阶段的短棍子的合并付出的代价和前一阶段由哪些棍子已经被合并有关，这应该是一个**区间DP问题**；

分阶段合并小区间具有某种代价
代价和前面的阶段有关

随手排序，发现cuts数组天然维护一个前缀和的形式：

以样例n = 7, cuts = [1,3,4,5]来说，最终分的短棍子长度只可能是1,2,1,1,2，那么其前缀和为0,1,3,4,5,7,我们每一阶段合并棍子的代价应该是某个长棍子的长度，也就是某个区间和,我们重新在cuts的头部插入0,尾部插入n;

假设cuts原始长度为m, 原子棍子的索引从1开始，一共有m+1个原子棍子，插入0,n后cuts长度为m+1;

在第len个阶段，合并索引在[i,j]中的棍子代价为cuts[j]-cuts[i-1]，这里j-i+1=len,他应该和上某个阶段区间合并有关，转移方程如下：

时间复杂度为;

AC代码

class Solution {
public:
    int minCost(int n, vector<int>& cuts) {
        sort(cuts.begin(), cuts.end());
        int m = cuts.size();
        vector<int> c;
        c.push_back(0);
        for(int i=0;i<m;i++) c.push_back(cuts[i]);
        c.push_back(n);

        int f[105][105]={0};
        for(int i=1;i<=m+1;i++){
            for(int j=i+1;j<=m+1;j++) {
                f[i][j]=INT_MAX;
            }
        }
        for(int len=2;len<=m+1; len++) {
            for(int i=1;i<=m-len+2;i++){
                int j=i+len-1;
                for(int k=i;k<j;k++) {
                    f[i][j]=min(f[i][k]+f[k+1][j]+c[j]-c[i-1], f[i][j]);
                }
            }
        }
        return f[1][m+1];
    }
};